Expand the formula of (xy)^3 Get the answers you need, now!Example Expand 3 × (52) Answer It is now expanded We can also complete the calculation 3 × (52) = 3 × 5 3 × 2 = 15 6 = 21 In Algebra In Algebra putting two things next to each other usually means to multiply So 3(ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbers👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms or

Expand X Y 3 Solved
(x-y)3 formula
(x-y)3 formula-If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions3 Answers3 For the nontrivial interpretation, you're looking for nonnegative solutions of a b c = n (each of these corresponds to a term x a y b z c ) Code each of these solutions as 1 a 0 1 b 0 1 c, for example ( 2, 3, 5) would be coded as Now it should be easy to see why the answer is ( n 2 n)




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic
Result A sum containing 2 terms;In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveSo to find the expansion of (x − y)3, we can replace y with (−y) in (x y)3 = x2 3x2y 3xy2 y3
The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative Y close parenthesis;The exponent is two;There are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –
(x y) 5 (x – y) 5 = 25C 0 x 5 5C 2 x 3 y 2 5C 4 xy 4 = 2(x 5 10 x 3 y 2 5xy 4) Now (√2 1) 5 (√2 − 1) 5 = 2(√2) 5 10(√2) 3 (1) 2 5(√2)(1) 4 =58√2 Binomial Expansion Important points to remember The total number of terms in the expansion of (xy) n are (n1) The sum of exponents of x and y is always nThe perfect cube forms (x y) 3 (xy)^3 (x y) 3 and (x − y) 3 ( xy)^3 (x − y) 3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them oftenThe second term of the sum is equal to a
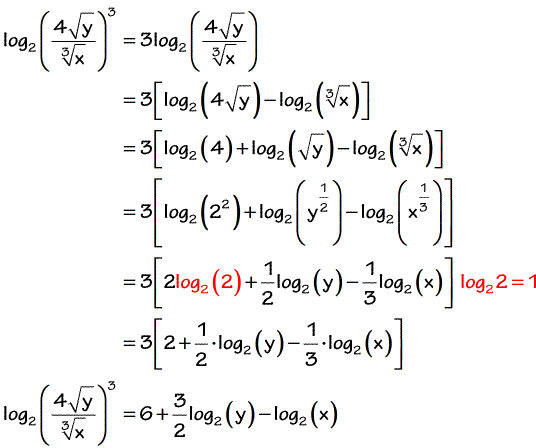



Expanding Logarithms Chilimath



1
The base is X;So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We know the algebraic expansion of (x y) 3 Rearranging the terms in the expansion, Substituting the values of x and y in the formula, Thus, we have factorized aDifferentiating by x the above formula n times, then setting x = b gives ()!




Expand X Y 3 Solved



4 The Binomial Theorem
Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! A set of coefficients of the terms in the expansion of the binomial that is correct is this is because if you do (x y)^3 or (x y) (x y) (x y) it is equal to x^3 3x^2y 3xy^2 y^3 remembering that the coefficient is what comes before the variable(x y) 3 = x 3 3x 2 y 3xy 2 y 3 (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




Ud69buhkaoxm M
Free expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using thisIn mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms (x y) 3 = x 3 y 3 3 x 2 y 3 x y 2Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
( xy)^3= x^3y^33xy(xy) IT IS THE EXPANSION FOR THE IDENTITY NOTE IF IN PLACE OF ( xy)^3 even if ( ab)^3 is given it is the same thing JUST NOTE THAT THE BASIC FORMUALA SHOULD BE THE SAME , OTHERWISE IT CAN BE ANY 2 DIFFERENT VARIABLES OR ANY 2 DIFFERENT NOS3 4 5 6 7 8 9 0, < > ≤ ≥ ^ √ ⬅ F _ ÷ (* / ⌫ A ↻ x y = G If we wanted to expand \({(xy)}^{52}\), we might multiply \((xy)\) by itself fiftytwo times This could take hours!




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo




What Is The Formula Of Math A B 3 Math Quora
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)This calculator can be used to expand and simplify any polynomial expressionWe pick one term from the first polynomial, multiply by a term chosen from the second polynomial, and then multiply by a term selected from




What Is The Formula For A B 6 Quora




X 2 3 Expand Formula Novocom Top
The Binomial theorem tells us how to expand expressions of the form (ab)ⁿ, for example, (xy)⁷ The larger the power is, the harder it is to expand expressions like this directly But with the Binomial theorem, the process is relatively fast!1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so not here 1Transcribed Image Textfrom this Question (a) 3 points Find the expansion of (xy)5 using using the binomial theorem (b) 13 points) What is the coefficient of z9 in (2 z)1?




A B N And A B N Formula Expander




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Trigonometry Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube of difference (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Difference of two cubes x 3 y 3 = (x y) (x 2 xy y 2) We've detected that you're using adblocking software or servicesBinomial Theorem For any positive integer , Combinatorial Proof Since each term in has the form for some between and , inclusive The coefficient of for a particular is just the number of ways to choose factors of from the factors of , with factors of coming from the remaining factors The number of ways to choose objects from a collection of




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
Using the Formula of Expansion of Binomial of Power 3 Examples Question 1 Find x 3 y 3, if x y = 5 and xy = 14 Solution x 3 y 3, if x y = 5 and xy = 14 (a 3 b 3) = (a b) 3 3ab(a b) (x 3 y 3) = (x y) 3 3xy(x y) By using the given values, we get (x 3 y 3) = 5 3 3= and so the power series expansion agrees with the Taylor series Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges to the value of the function at each point of the disk The simplify command finds the simplest form of an equation Simplifyexpr,assum does simplification using assumptions Expandexpr,patt leaves unexpanded any parts of expr that are free of the pattern patt ExpandAllexpr expands out all products and integer powers in ant part of exps ExpandAllexpr,patt avoids expanding parts of expr that do not contain terms matching




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic
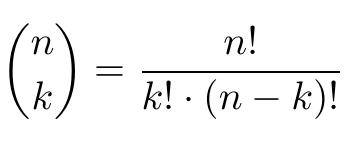



Binomial Coefficient Calculator
(c) 4 points The row of Pascal's triangle containing the binomial coefficients 0Now, we have the coefficients of the first five terms By the binomial formula, when the number of terms is even, then coefficients of each two terms that are atStart your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero Cancel



1
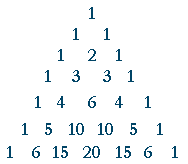



Binomial Theorem Topics In Precalculus
A 3 − b 3 = ( a − b) ( a 2 a b b 2) Then with the choice a = ( x y) 1 / 2, b = ( x − y) 1 / 2, and in the case x ≥ y , we can also write x y = a 2, x − y = b 2;Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, it #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#




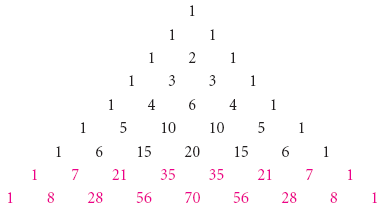
Pascal S Triangle And The Binomial Theorem




How Do You Expand X Y 6 Using Pascal S Triangle Socratic
Binomial Theorem to expand polynomials explained with examples and several practice problems and downloadable pdf worksheet (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;A binomial is a polynomial with exactly two terms The binomial theorem gives a formula for expanding \((xy)^n\) for any positive integer \(n\) How do we expand a product of polynomials?(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x *



Is There A Shortcut To Expand The Equation X Y Quora




Binomial Theorem Wikipedia
Put XY = A (AZ)^3= A^3 Z^3 3AZ ( AZ) = (XY)^3 Z^3 3 A^2 Z 3A Z^2 = X^3Y^3 Z^3 3 X^2 Y 3 X Y^2 3 (XY)^2 Z 3 (XY) Z^2 =X^3 Y^3 Z^3 3 X^2Y 3XY^2 3 ( X^2 Y^2 2XY ) Z 3X Z^2 3YZ^2 =X^3Y^3Z^3 3X^2 Y3XY^2 3X^2 Z 3Y^2 Z 6XYZ 3XZ^2 3 YZ^2 Arrange in order 97K viewsYou can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we can write we know that what is the formula of need too write in simple form of multiplication Simplify the all Multiplication one by one 0 Follow 0 A K Daya Sir, added an answer, on 25/9/13 A K Daya Sir answered this x 3 y 3 = (x y) (x 2 xy y 2 ) this formula can be derived from (x y) 3 = x 3 y 3 3xy (x y) x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) (x y) 2 3xy = (x y) x 2 y 2 2xy 3xy = (x y) (x 2 xy y 2 ) Was this answer




A Quick And Efficient Way To Expand Binomials Ppt Download




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9
An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for theirWhy create a profile on Shaalaacom?1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information
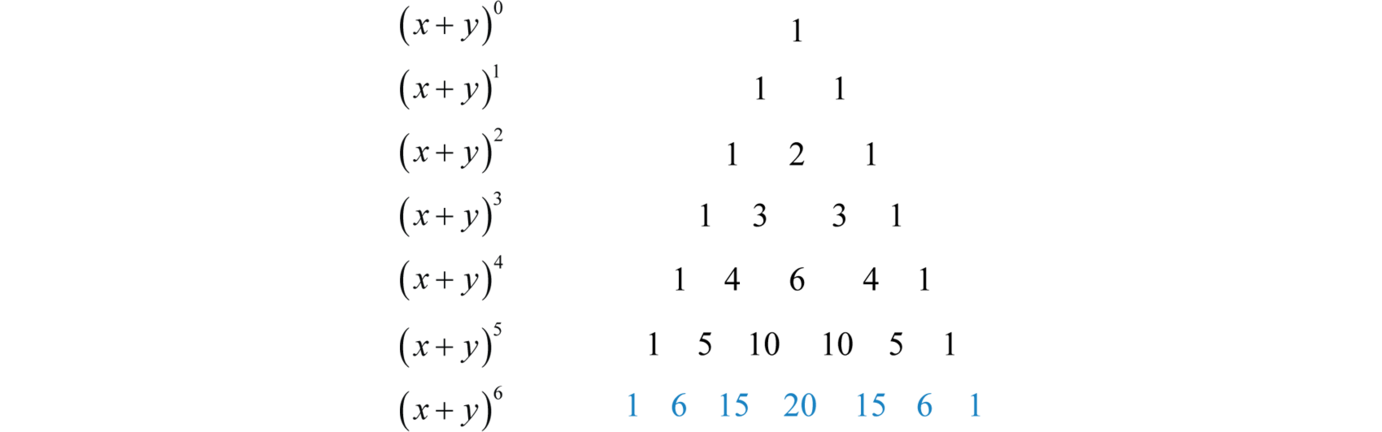



Binomial Theorem



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
If a binomial expression (x y) n is to be expanded, a binomial expansion formula can be used to express this in terms of the simpler expressions of the form ax by c in which 'b' and 'c' are non negative integers The value of 'a' completely depends on the value of 'n' and 'b'We're going to look at the Binomial Expansion Theorem, a shortcut method of raising a binomial to a power (xy) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 (xy) 5 = x 5 5x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 y 5 There are several things that you hopefully have noticed after looking at the expansion The n and r in the formula stand(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2 x 3 y ) 4




How Do You Expand The Binomial X Y 5 Socratic




Expand The Given Expression 3 X3 X Y 4 Z 33 X Gauthmath
x^33x^23x1 "note that" (xa)^3=x^3(aaa)x^2(aaaaaa)xa^3 (x1)^3toa=1 rArr(x1)^3=x^3(111)x^2(111)x(1)^3 =x^33x^23x1Answer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website!We are technically FOILing this out with a power of 3 (xy)(xy)(xy) So we can first factor out the first two "xy"s, multiplied by the last "xy" Coefficients are the number that comes in front of a variable In this case, 1 comes in front of , 3 comes in front of , 3 comes in front of , and 1 comes in front of Thus 1, 3, 3, 1



Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3
The Binomial Theorem is a formula that can be used to expand any binomial (xy)n =∑n k=0(n k)xn−kyk =xn(n 1)xn−1y(n 2)xn−2y2( n n−1)xyn−1yn ( x y) n = ∑ k = 0 n ( n k) x n − k y k = x n ( n 1) x n − 1 y ( n 2) x n − 2 y 2 ( n n − 1) x y n − 1 y nThe binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?For jxj < 1 (1) We call the power series the power series representation (or expansion) for the function f (x)= 1 1¡x about x =0 It is very important to recognize that though the function f (x)=(1¡x)¡1




Binomial Theorem Wikipedia




Section 8 5 The Binomial Theorem Ppt Download
Let us start with the formula 1 1¡x = X1 n=0 xn;Hence a − b = a 2 − b 2 a b = ( x y) − ( x − y) a b = 2 y a b, and a 2 a b b 2 = 2 x ( x 2 − y 2) 1 / 2The first term of the sum is a power;




Binomial Theorem




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Binomial Theorem Wikipedia




Taylor S Series Expansion An Overview Sciencedirect Topics



2
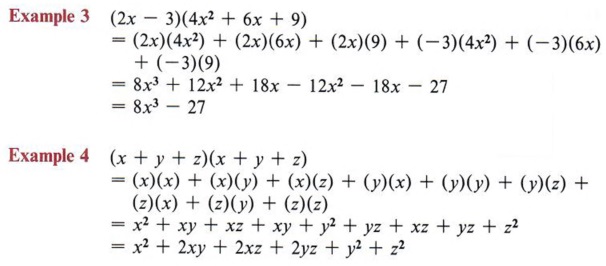



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Solution Find The Term Involving X 2 In The Expansion Of X 3




A B Formula Identity




The Binomial Theorem Defining Expressions Video Lesson Transcript Study Com




X Y 2 3 Find The Expansion Of The Following Brainly In




Expand And Simplify Binomial Squares 2x 3y 2 Youtube



1
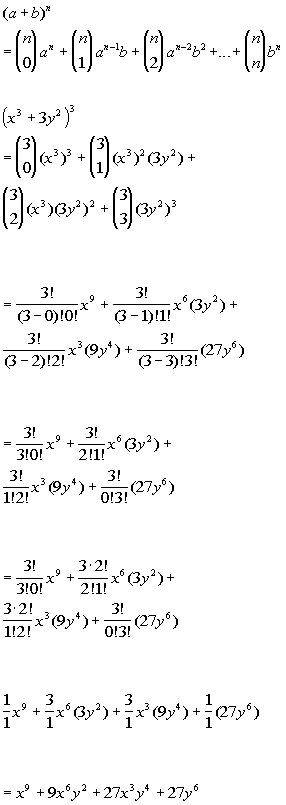



Tutorial 54 The Binomial Theorem




How To Calculate X Y N With Pascal S Triangle 9 Steps




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




Binomial Expansion Formulas Derivation Examples




X Y Z 3 Identity Novocom Top




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Expand 1x Y3 3 Maths Questions



What Is The Binomial Expansion For 1 X 1 Quora



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf




Section 8 5 The Binomial Theorem Ppt Download



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Solved Question 2 46 Marks 2 1 Expand And Simplify The Chegg Com




Binomial Coefficient Wikipedia




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
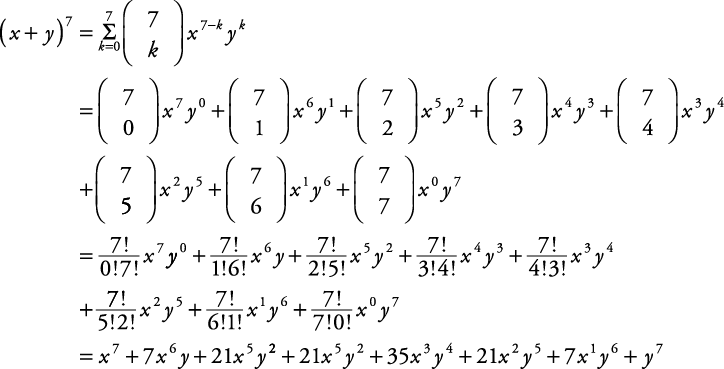



Binomial Coefficients And The Binomial Theorem




Expanding Logarithms




Expanding Algebraic Expressions Using Identities Worksheets



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf




Table 1 From Generalized Ismail S Argument And F G Expansion Formula Semantic Scholar
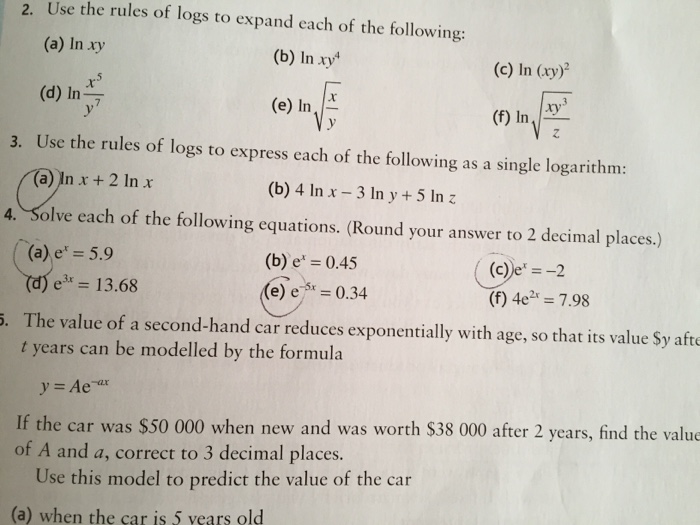



Solved 2 Use The Rules Of Logs To Expand Each Of The Fol Chegg Com
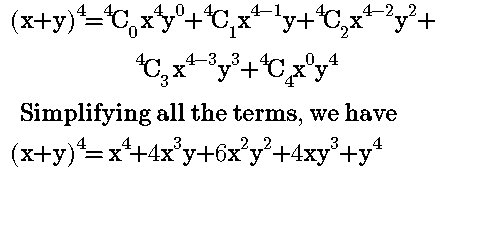



Worked Examples On Binomial Expansion Steemit




X Y 3 Identity Novocom Top
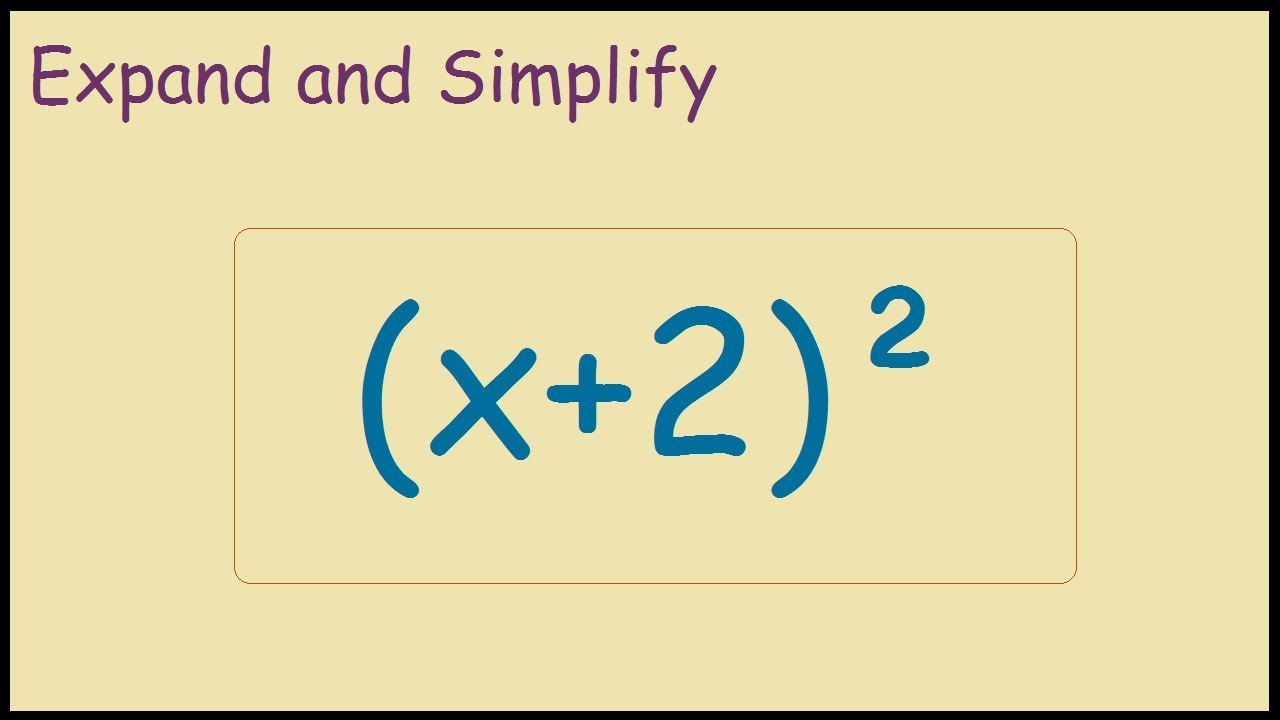



X 2 2 Expand And Simplify Using Foil Method Youtube




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Factorials To Binomial Theorem
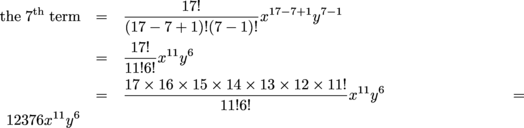



Pascal S Triangle And The Binomial Theorem



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University



A Lesson In Making Use Of Structure From With Jmccalla1 Experiments In Learning By Doing




Three Variables Cubic Polynomial Formulas Quadratics Maths Solutions Quadratic Equation




Using The Binomial Theorem College Algebra



1
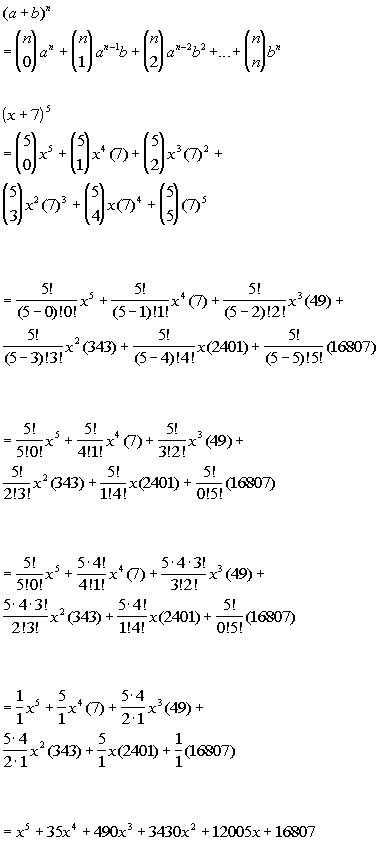



Tutorial 54 The Binomial Theorem




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange




Binomial Theorem




Expand 1 X Y 3 3 Solve It Fastly Brainly In
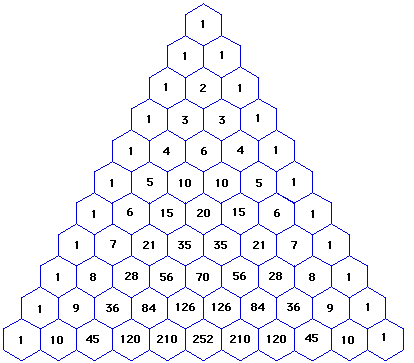



How Do You Expand X Y 10 Socratic




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
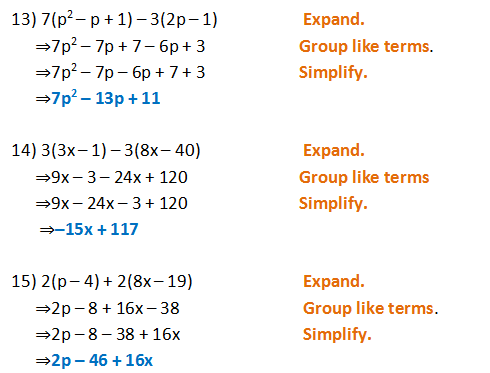



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths



Factorials To Binomial Theorem



What Is The Answer Of X Y Quora
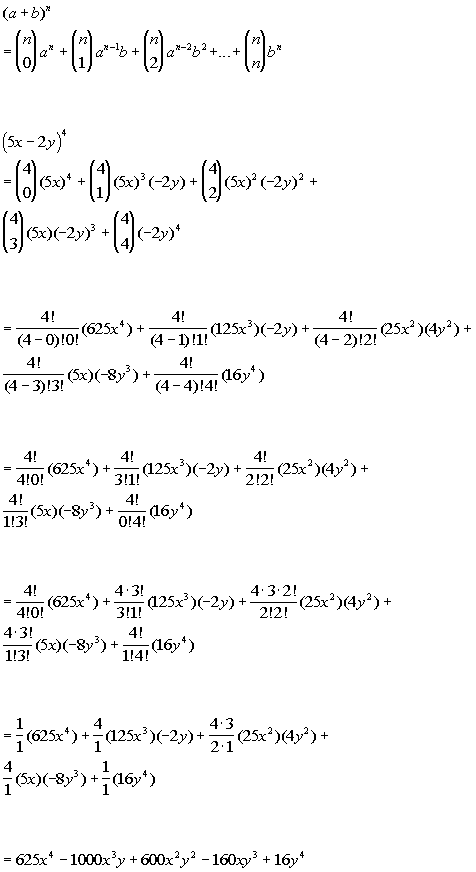



Tutorial 54 The Binomial Theorem




How To Calculate X Y N With Pascal S Triangle 9 Steps




9 5 The Binomial Theorem




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



What Is The Binomial Expansion For 1 X 1 Quora




Binomial Theorem For Any Index




Solved Section 33 Binomial Coefficients 30 Points 5 Bonus Points 12 Find Expansion X Y 5 Using B Q




Expanding Binomials Video Series Khan Academy



Expand 1 X Y 3 Whole Cube Studyrankersonline



Factorials To Binomial Theorem




Polynomial Expansion And Pascal S Triangle Ck 12 Foundation




Using The Binomial Theorem College Algebra




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



0 件のコメント:
コメントを投稿